吊橋の支柱の高さでワイヤーのテンションは変わるか

ゴールデンゲートブリッジ!!
きれいですね〜。迫力があります。
ところで、この橋の近くには、模型が置いてあって、橋の仕組みを体験できるようになってます。
力学の体験型模型。高さの違いでテンションがどう変わるかを体験できる…んだけど、真ん中の奴しか機能しておらず、肝心の比較ができない。 pic.twitter.com/GLbkn0rk84
— 岡竜之介(オブジェクション!の提案) (@agajo) 2016年9月29日
クイズにしてみましょう。力学の問題です。吊橋の支柱が高いほど、メインワイヤーにかかるテンションの大きさは
— 岡竜之介(オブジェクション!の提案) (@agajo) 2016年9月29日
最近ツイッターでこんな出題をしましたが、改めてこれについて考えてみましょう。
なんでせっかくサンフランシスコまで来て物理の問題出してんだよ!って話ですが
サンフランシスコサイドが橋の物理的な話を押してきてるんだからしょうがない。

ほらね。(サンフランシスコのゴールデンゲートブリッジのすぐ近くにある模型)
ということで、問題をもう一度ちゃんと乗せましょう。
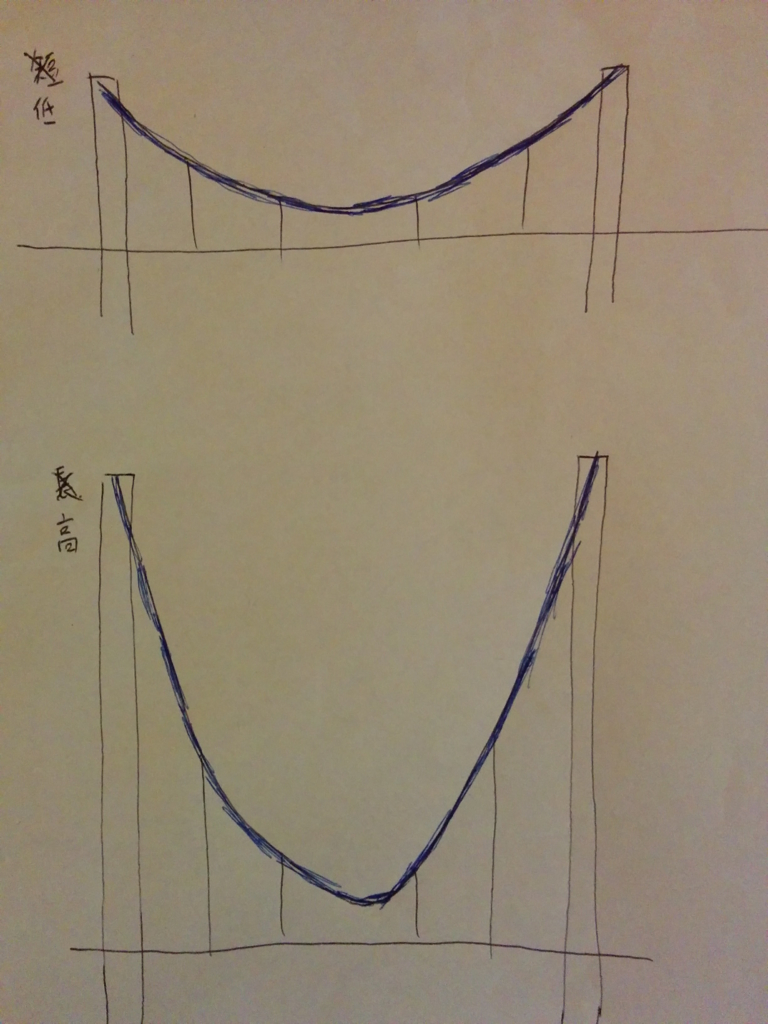
図のように、吊橋の支柱の高さを高くした時、メインワイヤー(青く太い奴)にかかるテンション(張力)は、大きくなるか、小さくなるか、変わらないか、という問題です。
ここで、ツイートで言及していなかった点をいくつか補足します。
(そこがわかってたらアンケートの解答違ってたよ〜〜という方、すいません。なんとか心の折り合いをつけて許してください)
補足1.
比較するテンションは、支柱と繋がってる部分で測定することにします。
補足2.
メインワイヤーのたらし具合は、支柱の長さに合わせてちょうど良く調整するものとします。
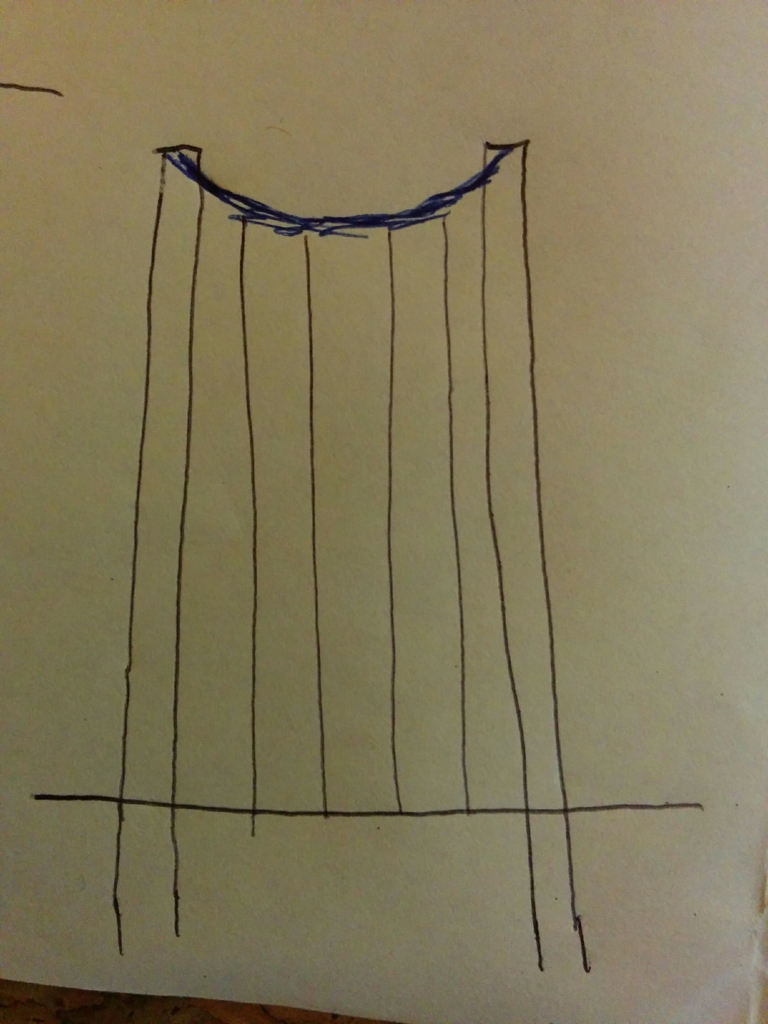
こういう橋は考えないってことです。(支柱は長くしたのに対してメインワイヤーが不自然に上にある)
補足3.
橋の重さは変わらないものとします。
厳密に言うと、メインワイヤーが支えなければならない重量が変わらないものとします。
さてみなさん。
考えましたでしょうか?
ではここから解説編です。
支柱の最上部でメインワイヤーにかかるテンションを考える時、
重要なのは、ここの角度なんですね。
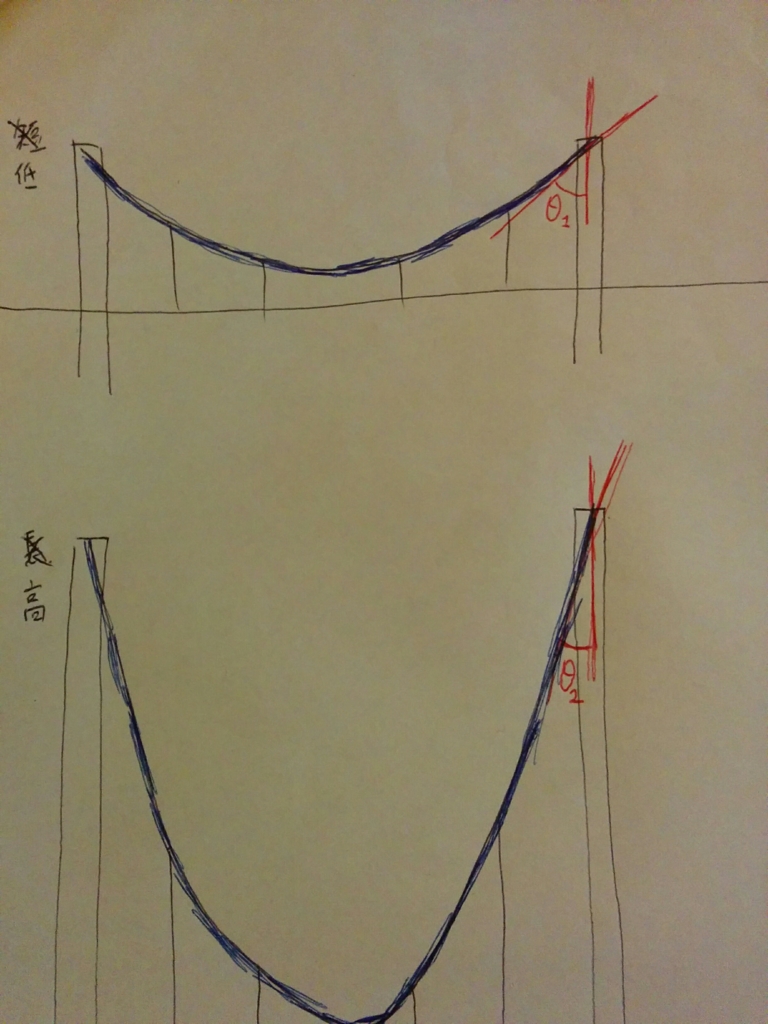
ここの角度さえキープしておけば、それ以外の構造はこんなふうにしても大丈夫です。
…大丈夫というのは、この問題を解く上で問題ないのであって、橋としての体裁はなくなってしまいますよ。
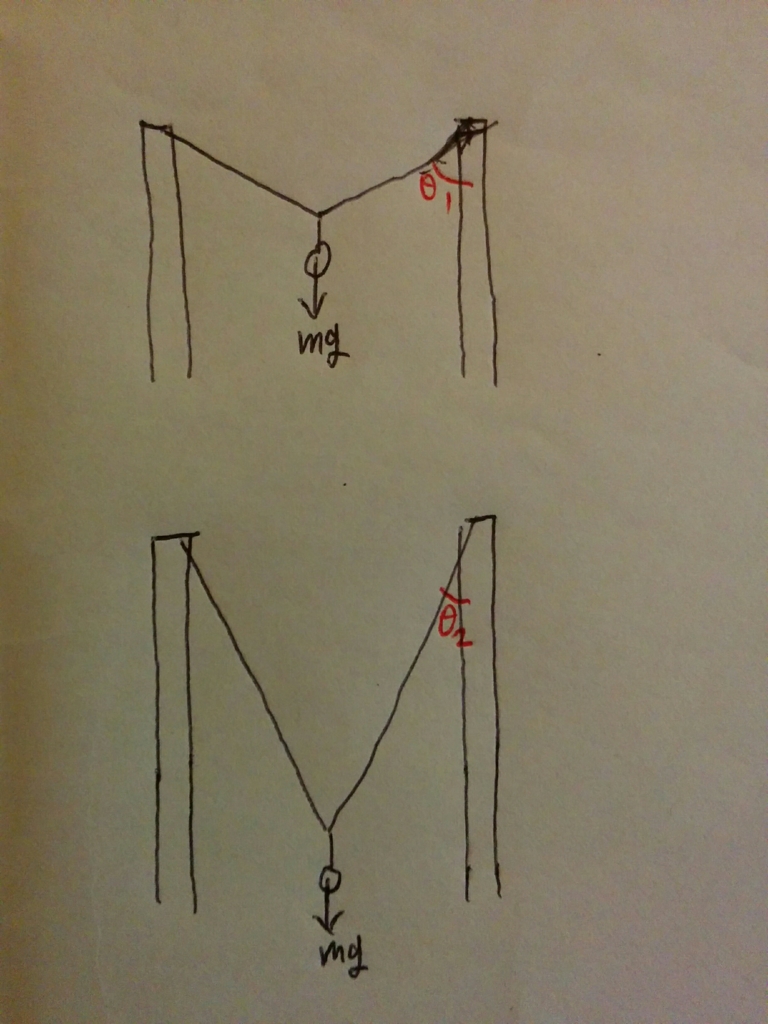
さらに、
・ワイヤーから支柱にかかってる力を書き込んで
・垂直方向と水平方向に分解してみます
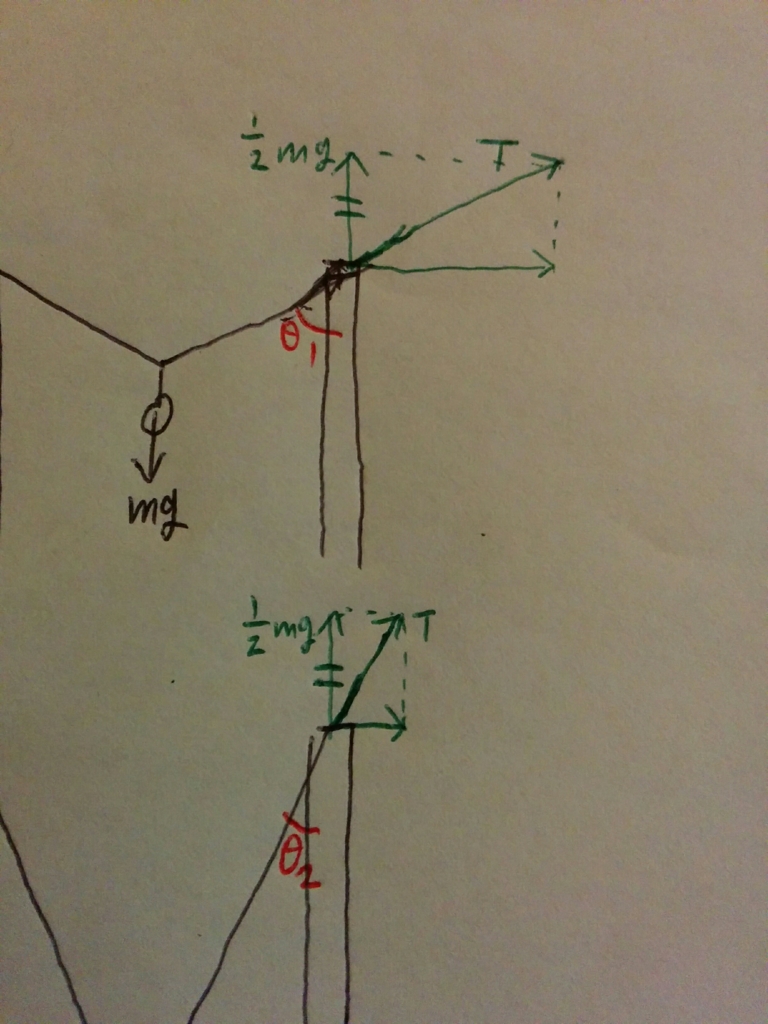
緑の長方形の、高さはどちらも(1/2)mgになります。
それに対して、それぞれの角度の方向にTを伸ばして、高さが(1/2)mgに達するようにするわけです。
Tが水平に近いほど、長くないといけないのがわかると思います。
Tの長さが長いということは、かかってるテンションが大きいということです。
なるほどね〜。
ということで!
支柱を高くすると、ワイヤーのテンションは小さくなります!
だから吊橋の支柱はやたらめったら高く作ってるんですね〜。
ちなみに完全に水平にすると、どれだけ引っ張ってもまったく持ち上がりません!そりゃそうだ!
ということでサンフランシスコにいるのに何故か物理ブログになりましたが、今回はここまで。
次回は観光地としてのゴールデンゲートブリッジを紹介したいと思います笑