のぺーっと分布した超関数 - 岡竜之介のブログ

ディラックのデルタ関数

ディラックのデルタ関数ってあるじゃないですか。

はい。まあもちろん知らない人が大半です。なのでちょこっと説明します。

デルタ関数の定義

定義はこちら。

${\displaystyle \int_{-\infty}^{\infty} f(x) \delta (x) dx = f(0) }$

これを満たす ${\delta (x)}$ をデルタ関数といいます。

ちなみに関数ではありません(!)。

関数に似てるけど、関数としては性質がふざけてるので、「超関数」という分類になってます。

これに ${f(x) = 1}$ を代入すると

$\int _{-\infty}^{\infty} \delta (x)dx = 1$

がわかります。マイナス無限大から無限大まで積分すると1になるなんて、確率分布(確率密度関数)みたいですね。

確率密度関数列の極限としてのデルタ関数

実はデルタ関数は他の確率密度関数から類推してやると理解しやすいです。

2つ紹介します。

正規分布の分散→0にしたもの

${\displaystyle a_n (x) = \frac{1}{\sqrt{2 \pi \left(\frac{1}{n}\right)^2 } } \exp \left( - \frac{x^2}{2 \left(\frac{1}{n}\right)^2 } \right) }$

分散が ${\left(\frac{1}{n}\right)^2}$ となってます。

こいつの ${n}$ を大きくしていくと…

f:id:agajo:20170317201037g:plain

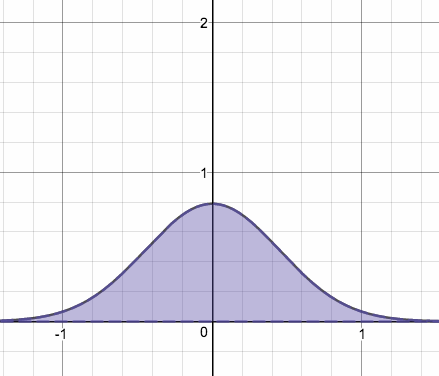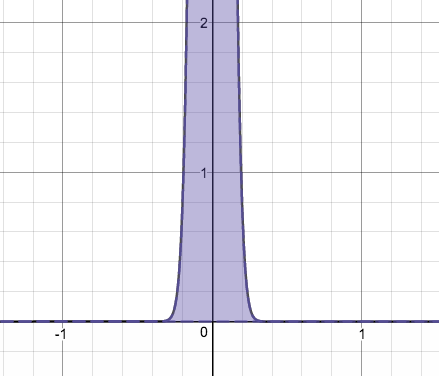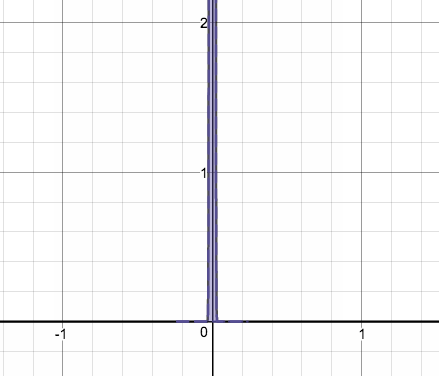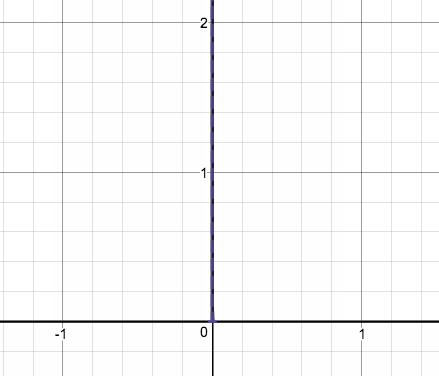
あ、1つめの関数がどの位置にあるかとか、nが大きくなる時の変化の幅とかは適当です。

要するにどういう動きをするのかってことだけわかれば良いので。以下同様。

一様分布の幅を→0にしたもの

${\displaystyle \begin{eqnarray} b_n(x) = \left\{ \begin{array}{ll} n/2 & (-1/n \leqq x \leqq 1/n) \\ 0 & (otherwise) \end{array}\right. \end{eqnarray} }$

一様分布の範囲の幅が ${2/n}$ になってます。

この ${n}$ を大きくしていくと…

f:id:agajo:20170317202755g:plain

という感じ。

どちらの場合も、面積=1 をキープしたまま、y軸にピッタリと張り付いていく様子がわかりますね。

関数列の収束について

${a_n(x)}$ も ${b_n(x)}$ も ${f(x)=0}$ に各点収束します。でも一様収束はしません。

各点収束とか一様収束については解説すると長くなるのでここでは割愛するので、知らない人は流し読みしてください。

ちなみに、一様収束する場合は、積分範囲が有限の場合、積分してから極限とるのと極限とってから積分するのとで、結果が同じになるらしいです。

今回は、先に積分すると1だし(nに関わらず面積1だから)、先に極限とると0になる(f(x)=0になるから)ということで、積分してから極限とるか極限とってから積分するかで値が違いますね。

一様収束してないし、積分範囲が有限でもないですからね。

確率密度関数としてのデルタ関数

例えばですね、これを「x軸上で、ある粒子がどの位置にあるか、という確率を表す」と解釈することが出来るわけですよ。

そしてデルタ関数の場合、「100%絶対に ${x=0}$ の地点にある」と断言できるわけです。

普通、x軸という連続な範囲において、ある厳密な一点に粒子がある確率は0%です。ほんのちょっとでもズレてたらアウトなので、そういうことになるんです。

「 ${0 \leqq x \leqq 1}$ の範囲にある確率」みたいに範囲で考えて初めて、意味のある確率が出てくるわけです。

なのに、デルタ関数の場合は、厳密に ${x=0}$ の地点にあると断言できるので、気持ち悪いわけですね。

このあたりからも、デルタ関数が普通の関数ではなくて超関数であることがわかります。

累積分布関数

累積分布関数というのは、確率密度関数をマイナス∞からxまで積分してきた値を示したものです。

「あるx以下の範囲に粒子がある確率」を表します。なので、xが ${-\infty \to \infty}$ と変化するとき、累積分布関数は 0→1 と変化します。

ちなみにデルタ関数を確率密度関数と考えた時の累積分布関数はこうなります。

f:id:agajo:20170317203059p:plain

${x=0}$ でピョンと飛び上がります。 ${x \lt 0}$ の時はその範囲に粒子はないし、 ${0 \lt x}$ の時は100%その範囲に粒子があるわけです。

厳密に ${x=0}$ の上でどうなってるかは知りません。多分どうでもいいです。

のぺーっとした超関数を考えよう！

ここまでデルタ関数を紹介してきました。

これに対して、のぺーっとした超関数はないのか、というのが今回の疑問。やっと本題ですよ！！

やっとって言っても、texで式書いたりgif動画作るのに時間がかかったのは僕の話であって、読んでると一瞬かもしれないですけどね！！

はい。

「のぺーっとした関数」でググっても、ツイッターで聞いてみても、全然それっぽい話がヒットしなかったので、調べるのは諦めて自分で考えることにしたのが事の発端です。

まず名前を付けよう！

デルタ関数にならって、イプシロン関数と呼びましょう。

${\displaystyle \epsilon (x) }$

ってわけです。

「イプシロン関数」で検索しても既存のものはなかったので、良いでしょう。

確率密度関数列の極限としてのイプシロン関数

まずはデルタ関数の時と同様に、確率密度関数の極限を使ってイメージを掴もう！

正規分布の分散→∞にしたもの

${\displaystyle c_n (x) = \frac{1}{\sqrt{2 \pi n^2 } } \exp \left( - \frac{x^2}{2 n^2 } \right) }$

分散が ${n^2}$ となってます。

こいつの ${n}$ を大きくしていくと…

f:id:agajo:20170317204548g:plain

こう。

一様分布の幅を→∞にしたもの

${\displaystyle \begin{eqnarray} d_n(x) = \left\{ \begin{array}{ll} 1/2n & (-n \leqq x \leqq n) \\ 0 & (otherwise) \end{array}\right. \end{eqnarray} }$

一様分布の範囲の幅が ${2n}$ になってます。

この ${n}$ を大きくしていくと…

f:id:agajo:20170317204941g:plain

どちらも面積=1をキープしたまま、x軸にのぺーっと張り付いていく様子が見て取れます。

関数列の収束について

このイプシロン関数を考えている時に不安だったのが、

これ、完全に ${f(x)=0}$ に一致してしまって、イプシロン関数なんてものを考えることはできないんじゃないか？

ということです。

0.999999.....が1と等しいみたいな。1と別個に0.99999.....という数字を考えることはできないわけです。

実際、この ${c_n(x)}$ とか ${d_n(x)}$ は、 ${f(x)=0}$ に一様収束します。

各点収束もするし、一様収束もするんです。

一様収束は、各点収束よりも割りとガッツリ収束していくので、極限とったら完全に同じものになるんじゃないか。

…と思ってたんですけど。

これ、nをどれだけ大きくしても積分はずっと1なんですよ。一方、 ${f(x)=0}$ は積分したら0です。

これは、はっきり違いますね。全然一致してないです。

先に極限とって積分するのと、積分してから極限とるのとで、値が違うわけですね。

積分と極限の順序を入れ替えてもいいのは「一様収束」「積分範囲が有限」という2つの条件がありましたが、

今回は、一様収束はしても、積分範囲が無限だから、積分と極限は順序を入れ替えたら値が変わりうるわけですね。

なるほど。

ということで。

どういう関数(超関数)のことを考えているか、大体伝わったと思います。

こいつの性質を調べよう！！！

確率密度関数としてのイプシロン関数

デルタ関数は
「x軸上で、ある粒子が100%絶対に ${x=0}$ に存在する。」
という確率を表していました。

それに対して。

イプシロン関数は
「x軸上で、ある粒子が存在する確率が、x軸上のありとあらゆる点で同様に確からしい」

と解釈するのが自然でしょう！！！！

…いや、「！」マークまで付けて強調しましたが、それが自然だと感じているのが僕だけだったらごめんなさい。

累積分布関数

イプシロン関数を確率密度関数と考えるなら、その累積分布関数を考えるのは自然な流れです。これは自然な流れです。

で、累積分布関数を考えてみるんですが…

これが、よくわからないんですよ！！

累積分布関数である以上、マイナス∞の極限で0、プラス∞の極限で1になります。これはイプシロン関数の性質「積分すると1」と合致します。

そして、その (-∞,0) と (∞,1) の2点を「水平な直線」で結んだものが、累積分布関数になると思われます。

…うん。いや、飛躍してますかね。どうですかね。

イプシロン関数の値自体はずっと(ほぼ?)0なので、その積分である累積分布関数は傾き(ほぼ?)0の線なわけです。つまり(ほぼ?)直線です。

「(ほぼ?)」といってるのは、厳密に0なのかどうなのか僕がよくわかってないからです。

いやだって厳密に0だったら積分が1にならないじゃない！でも有限の値とってかつx軸全体で同様に確からしかったら、積分が発散しちゃうのでやっぱり厳密に0だよなあ…。

まあいい。

とにかく、水平な直線ということで納得しましょう。

累積分布関数のグラフ

次の問題は、この累積分布関数のグラフを書こうとすると発生します。

x=0の時の累積分布関数の値がわからないので、水平な直線をどの辺に書いたらいいのかわからないんです！

f:id:agajo:20170317230026g:plain

「いや、普通に ${y=1/2}$ じゃないの？」と思った方もいるかもしれません。

でも、それって正しくないと思うんですよ。

${x=0}$ で ${y=1/2}$ という考え方は、 ${x=0}$ が「真ん中」だからっていう感覚から来てると思うんですけど

「真ん中」って何？　という話なわけです。

粒子の存在確率はx軸上全体で同様に確からしいわけだから、 ${x=0}$ を「真ん中」とかいう「特別」な扱いをする必然性はどこにもないわけです。

宇宙に中心はない、みたいな話ですね。

イプシロン関数を定義しよう

とまあ、感覚的な話が続いてしまいましが

数学の記事を書いてるのに感覚的な話に終始していてはいけません。

累積分布関数がどこを通るかわからないのは、きっとイプシロン関数をちゃんと数式で定義していないからなのでしょう。

ということで、定義を試みます。

デルタ関数の

${\displaystyle \int_{-\infty}^{\infty} f(x) \delta (x) dx = f(0) }$

みたいに、他の関数と掛け算して積分した時にどうなればいいか、っていう観点で定義できそうかな？

${\displaystyle \int_{-\infty}^{\infty} f(x) \epsilon (x) dx = ??? }$

どうなればいいんでしょうね。

また感覚的でアレですが、この積分は「 ${f(x)}$ の平均値」を表していると考えられます。

それも普通の平均ではなく、(-∞,∞)という範囲における平均です。

(-∞,∞)という範囲において、イプシロン関数は「同様に確からしいという確率」を表すわけですから、それと ${f(x)}$ を掛け算して積分したら、f(x)の平均値がでるんです。

「値×確率」を全部足すって奴です。説明が超雑ですが、ここで確率論の説明してると長くなるのでこの程度にします。

さて。

まず、 ${f(x)=1}$ の時は、この積分は1になってなきゃいけません。

${\displaystyle \int_{-\infty}^{\infty} \epsilon (x) dx = 1 }$

というわけです。イプシロン関数に要求している性質です。まあそれはいい。

${f(x)}$ が定数の時は、その定数がそのまま積分値になりますね。まあそれもいい。

${f(x) = x }$ の場合はどうでしょう？

${\displaystyle \int_{-\infty}^{\infty} x \epsilon (x) dx = ??? }$

この積分は、x軸上で粒子が発見される位置の「期待値」を表します。「値×確率」を全部足すっていう奴です。

この積分はどうなるでしょうか？

${x=0}$ の左半分と右半分で相殺するから、積分結果は0…？

…。

はい、違いますね。

その考え方は、 ${x=0}$ を「真ん中」と捉えている場合の考え方です。

${x=3}$ を「真ん中」としてその左右が相殺すれば、積分値は3になるわけです。

結局、この積分が「わからない」んですよね。宇宙に中心はないわけです。

ということで、

${\displaystyle \int_{-\infty}^{\infty} x \epsilon (x) dx = ??? }$

の「???」の部分、ひいては

${\displaystyle \int_{-\infty}^{\infty} f(x) \epsilon (x) dx = ??? }$

の「???」の部分が埋められないので、これうまく定義できないですね。

いや、方法はあるのかもしれないけど、今の僕ではうまく扱えません。

そして、実際、うまく扱う方法がなくて何の役にも立たないから、この関数は検索してもヒットしなかったのかもしれません。

そんな気がします。

…

……

………

いや、まだだ！！！！！！！

デルタ関数だって、 ${x=0}$ を特別な点として扱っていたじゃないか！！

イプシロン関数でも、 ${x=0}$ を特別な点として扱ってみたらどうだ？

主観的に中心を決めてしまえば良いわけですよ。

だって、あなたがこの宇宙にある何かを感じる時、どうしたってそれはあなた一人が感じているわけで

他の人とまったく同じ感じ方をしていることはありえないわけで

相対性理論だって観測者によって時間の感じ方とか質量とかが変わるって言ってるわけで

まあ要するに

宇宙の中心はある！！

それはお前自身だ！！

いや、むしろ、この文を書いている俺からしたら、宇宙の中心はお前ですらない

宇宙の中心は、常にこの俺だ！！！

というわけでですね。

まったく飛躍のない極めて論理的な推論によって、 ${x=0}$ を特別扱いすることが根拠付けされました。

今度こそイプシロン関数を定義する

${\displaystyle \int_{-\infty}^{\infty} f(x) \epsilon (x) dx = \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} f(x) dx }$

はい。いきなりでアレですが、これでしょうね。

右辺の積分範囲がポイントです。

プラス側とマイナス側に、 ${x=0}$ を「真ん中」として、同じ速度で積分範囲が大きくなるようになっています。

そして、その積分範囲の幅で積分値を割ることで、 ${f(x)}$ の ${(-t,t)}$ の範囲での平均値を出します。

最後に、その ${t}$ を ${\infty}$ にふっ飛ばすわけです。

積分が1か確認する

${f(x)=1}$ を代入します。

${\displaystyle \begin{align} \int_{-\infty}^{\infty} \epsilon (x) dx &= \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} dx \\ &= 1 \end{align} }$

完璧ですね。

f(x)にいろいろ入れてみる

f(x)にいろいろ関数をいれてみて、

それらの関数の「x=0を『真ん中』とした平均値」を求めてみましょう。

定数

${\displaystyle \begin{align} \int_{-\infty}^{\infty} a \epsilon (x) dx &= \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} a dx \\ &= a \end{align} }$

定数がそのままでてきました。実はこれデルタ関数と同じ性質です。

ずっと同じ値なんだから、その平均もその値になるに決まってますね。

1次式

${\displaystyle \begin{align} \int_{-\infty}^{\infty} (ax+b) \epsilon (x) dx &= \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} (ax+b) dx \\ &= b \end{align} }$

あれ、一次式の部分消えましたね！？

これは、上で述べた

「 ${x=0}$ の左半分と右半分で相殺するから、積分結果は0」

が起こってるわけです。

2次式

${\displaystyle \begin{align} \int_{-\infty}^{\infty} (ax^2 + bx + c) \epsilon (x) dx &= \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} (ax^2+bx+c) dx \\ &= \infty \end{align} }$

これ計算すると、無限大に発散します。

aが正なら正、負なら負の無限大に発散します。

多項式

計算しませんが、奇数次の項しかなければ0だし、2次以上の偶数次の項があれば正か負の∞に発散しますね。

結局、二次以上の項は絶対値がどこまでも大きくなるので、プラスとマイナスで相殺しない限り、その平均値は無限大になっちゃうわけですね。

指数関数

${\displaystyle \begin{align} \int_{-\infty}^{\infty} e^x \epsilon (x) dx &= \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} e^x dx \\ &= \infty \end{align} }$

これも発散します。二次式の時と話は同じです。

三角関数

${\displaystyle \begin{align} \int_{-\infty}^{\infty} \cos (x) \epsilon (x) dx &= \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} \cos (x) dx \\ &= 0 \end{align} }$

はさみうちの原理とかでアレすると、これ0になります。

三角関数はず〜っと ${y=0}$ の上下で揺れてるだけなので、それを全範囲で平均とると0になるわけですね。

累積分布関数を確認する

ヘヴィサイドの階段関数 - Wikipediaに書いてあるのと同じようにやってみます。

まず「指示関数」とかいうものを持ってきます。

${\displaystyle \begin{eqnarray} \chi_A(x) = \left\{ \begin{array}{ll} 1 & (x \in A) \\ 0 & (x \notin A) \end{array}\right. \end{eqnarray} }$

これです。範囲内にあれば1、なければ0。

これを使って、累積分布関数、つまり「マイナス無限大からxまでの積分」を

${\displaystyle \int_{-\infty}^x \epsilon (t) dt = \int_{-\infty}^{\infty} \chi_{(-\infty,x]} (t) \epsilon (t) dt }$

と定義します。

xより大きい所では、指示関数が0になってくれるので、結局右辺と左辺は同じ値になるはずですね。

ただし、あくまでも「マイナス無限大から『ある有限の値xまでの積分』」を定義しただけです。この点、覚えておいてください。

ところでこいつは、イプシロン関数の定義より

${\displaystyle \begin{align} \int_{-\infty}^x \epsilon (t) dt &= \int_{-\infty}^{\infty} \chi_{(-\infty,x]} (t) \epsilon (t) dt \\ &=\lim_{t \to \infty} \frac{1}{2t} \int_{- t}^{t} \chi_{(-\infty,x]} (s) ds \\ &=\lim_{t \to \infty} \frac{1}{2t} \left[ g(s) \right]_{-t}^{t} \\ &=\lim_{t \to \infty} \frac{1}{2t} (t+定数) \ \ (∵tが十分大きい時だけを考える) \\ &=\frac{1}{2} \end{align} }$

いきなりg(s)とかいうのが出てきましたが、指示関数 ${\chi_{(-\infty,x]} (s)}$ の不定積分(原始関数)です。
x以上の所では定数cで、xより小さい所では傾き1の直線(s-x+定数c)です。
xの関数ではなくてsの関数の話をしているので気をつけてください。この部分ではxは定数です。

ということで、やっと答えが出ましたが、累積分布関数はなんと ${\frac{1}{2}}$ です！！

まあ、上でも「水平な直線」と言ってたので、わかってたっちゃわかってたんですが、xに依存しないんですね！！

どっか適当なx軸上の点を持ってきて、「その点より左にある確率」を考えると、いつだって1/2だということです。持ってきた点が宇宙の真ん中になるわけですよ多分。おもしろっ。

x→無限大にしても1にならないけど？

累積分布関数はx→無限大とした場合1にならなければいけません。

でもこの 1/2 とかいう累積分布関数は、x→無限大にしてもずっと 1/2 ですね。

ここで思い出してほしいのが、上の定義はあくまで、マイナス無限大から『ある有限の値xまでの積分』」を定義しただけだったということです。

x→無限大とか、x→マイナス無限大の時については何も言ってないわけですよ。

有限の時しか成り立たないですよ、と断って話をしていたので、「無限にしたら矛盾するけど？」とか言われても「知らん。」というわけです。

じゅう無限の時はどうするのって話なんですけど、

x→無限大の時は1、x→マイナス無限大の時は0、って、定義すればいいんじゃないかな！それで完璧に条件を満たしますよ！！

極限とるタイミングをかなり気をつけて扱わなきゃいけない関数の完成ですね。これも超関数なのかな？

${\displaystyle \begin{eqnarray} E (x) = \left\{ \begin{array}{ll} 1/2 & (- \infty \lt x \lt \infty) \\ 0 & (x = - \infty) \\ 1 & (x= \infty ) \end{array}\right. \end{eqnarray} }$

粒子の位置を表す関数として解釈する

デルタ関数が「x=0に粒子がある」という確率を表していたので、イプシロン関数についても改めて解釈してみましょう。

…といっても、イプシロン関数から読み取れることは、「x軸全体のどこかにある」という情報だけです。「どこにある確率が高い」とかそういうことは何も言えません。

というのはまあ、そうなんですが

ここで、次の値を計算してみます。

${\displaystyle \int_{-\infty}^{\infty} x \epsilon (x) dx }$

この計算は、「粒子が存在する位置の期待値」を表します。

「値×確率」を全部足してるわけです。何回言ったっけこれ。

ただこれ、xって単なる一次式なので、上で計算したように、答え0なんですよね。

平均値としては、x=0になるんです。

宇宙の中心はあなたというわけですよ。つまりね。そういうこと。

ただ、決して「x=0に存在する確率が高い」とは言ってないことに注意してくださいね。

そうなってくると、「平均はx=0」の意味って何なんでしょうね。何か言えるんですかね。

xが正とxが負の部分で、どちらも確率が1/2なので、まあ、観測を何度も何度もやったら、平均はx=0に収束していくっていうことですかね。

ところがこれすごいのが、x=0の地点にいるあなたがやってもそうなるんですけど、

x=10の地点にいる高橋君が同じことをやってもそうなるんですよ。高橋くんにとってもやっぱり、自分を中心に粒子が発見されるわけです。

x=2億の地点にいるロドリゲスにとっても同じです。ロドリゲス中心に粒子が発見される。

わけわかんないですけど、そういうことなんですよ多分。

あなたにとって世界の中心はあなただけれども、高橋君にとっては世界の中心は高橋君なんです。あなたと高橋君は違う地点に立っているにも関わらず、です。

まあ、そういう前提を置いたんだから、この結果は当然なんですけどね。多分。

原点以外のところへずらす

ここから「EMANの物理学」のデルタ関数の記事を参考にしてます。
ネットで物理とか数学とか調べたことのある人はきっと知っている有名サイトです。
いや、まあ、ここまでも参考にしてたけど。

つーことで。

ε(x-a)について考えると

${\displaystyle \int_{-\infty}^{\infty} f(x) \epsilon (x-a) dx = \int_{-\infty}^{\infty} f(x'+a) \epsilon (x') dx' }$

x'=x-a です。

まあ、そうですね、x=aを「真ん中」とした時の f(x) の平均値がでます。上の高橋君とかロドリゲスとかの話の根拠ですね。

偶関数に似た性質

がんがん省略しますが、

定義式

${\displaystyle \int_{-\infty}^{\infty} f(x) \epsilon (x) dx = \lim_{t \to \infty} \frac{1}{2t} \int_{-t}^{t} f(x) dx }$

の右辺について

${\displaystyle \int_{-t}^{t} f(-x) dx=\int_{-t}^{t} f(x) dx }$

が言えるのと、左辺について

${\displaystyle \int_{-\infty}^{\infty} f(-x) \epsilon (x) dx = \int_{-\infty}^{\infty} f(x) \epsilon (-x) dx }$

が言えるのとかを使って、引き算したりすると

${\displaystyle \epsilon (x) = \epsilon(-x) }$

が言えます。ほえ〜。

「偶関数『に似た』」と言っている意味合いについては元サイトを御覧ください。

変数のスケールを変える

${\displaystyle \epsilon (ax) }$

について考えよう。

つってもまあ、普通に、横方向に 1/|a| 倍されるイメージで良くて

${\displaystyle \int_{-\infty}^{\infty}\epsilon (ax)dx = \frac{1}{\mid{a}\mid}\int_{-\infty}^{\infty}\epsilon (x)dx }$

です。|a|が1より大きいなら、面積が横方向に縮んでるわけです。普通の関数のイメージと変わらないですね。

これ、デルタ関数でも話は同じなんですが、元サイトに

「
${\displaystyle \delta (ax)dx = \frac{1}{\mid{a}\mid}\delta (x)dx }$

これは変だ。横から押し潰された結果としてなぜか高さが縮むことを表しているように思える。普通の ${f(x)=x^2}$ などのグラフと比べてしまうと逆のことが起きているイメージなのだが、こう考えないと辻褄が合わないので受け入れるしかない。
」

という記述があります(閲覧日2017-03-18)が、これ、積分記号を省略してるからですね。

積分記号を省略せずに解釈すれば、あくまでも横に縮むイメージのままで大丈夫です。

微分してみる

イプシロン関数の微分は、直感的に0でしょうよ！！

数式でちゃんと言えないか試してみよう。

…。

はい。

これ0じゃないですね。

こんな感じになりました。元サイトと同じ議論です。

${\displaystyle \begin{align} \int_{-\infty}^{\infty} f(x) \epsilon ' (x) dx &= \left[ f(x) \epsilon (x) \right]_{- \infty}^{\infty} - \int_{-\infty}^{\infty} f'(x) \epsilon (x) dx \\ &= - \int_{-\infty}^{\infty} f'(x) \epsilon (x) dx \end{align} }$